√ 画像 エントロピー 145392-画像 エントロピー 意味
エントロピー定義 確率変数Xのエントロピーを,「Xの事象の 情報量の平均」と定義する(実際, Xの「平均 情報量」とも言う) つまり Xのエントロピー H(X) = – p i log p iJun 04, 21q8:「ハイブリッド符号化」とは? h264/avcなどの、現代の画像圧縮符号化が利用する、「動き補償フレーム(画面)間予測」と「dct」に「エントロピー符号化」を組み合わせた「ハイブリッド符号化」について詳しく説明してください。エントロピーは集合Aの要素数を として である.言い換えると,「要素 が当たりである確率が であることを知っているときのエントロピーは である.」ともいえる.シャノンは右辺の式がエントロピー のより一般的な定義であると考えた. = ∑ =− ∑ ∈ −

エントロピー 計算 熱力学の基礎
画像 エントロピー 意味
画像 エントロピー 意味-エントロピー符号化 符号化:アルファベット(整数)列を0, 1の系列に直すこと。 符号:1つのアルファベットに割り当てられた0, 1の系列 例: 符号:0!00, 1!01, 2!1001 アルファベット列:11! エントロピー:平均情報量(符号の出現確率で決まる量) 平均符号長はエントロピー以下にはできない。Jpegでのエントロピー符号 dc成分: 画像成分について,ブロック内のベースとなる値 前のブロックのdc成分値との差(差分値)を記録する
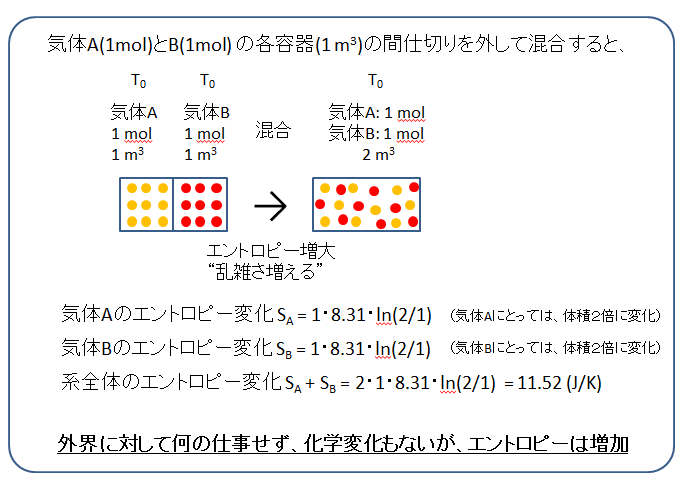



コース 物質が持つエネルギーの内訳 エントロピーと熱力学関数
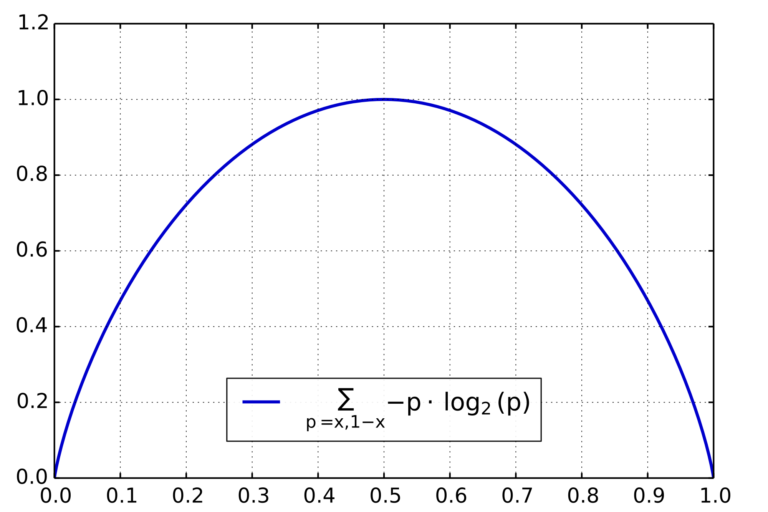
May 10, 21でエントロピーを定義できる。 ^ ボルツマン定数を1とする単位系を取れば、エントロピーは情報理論におけるエントロピー(自然対数を用いたもの)と完全に一致し、無次元量となる。 簡便なので、理論計算などではこの単位系が用いられることも多い。なお、この単位系では温度は独情報理論05 担当 大学院情報科学研究科井上純一 例題2 2 値エントロピー関数 H(p)=−plogp − (1 − p)log(1 − p) の最大値が1 であり, そのときのp の値がp =1/2 であることを学んだここでは, これをn 個の事象に拡張することを考えたい つの画像内の各画素(i,j)に対してCIEカラーシステムのX,Y,Z,L*,a*,b*,C*abおよびh。bが, それぞれの測定とこれらの値の適切な変換をすることにより求められたすべての画素に対するし*, エントロピー(ENT)およびフラクタル次元(D)が視覚的特徴量として測定された
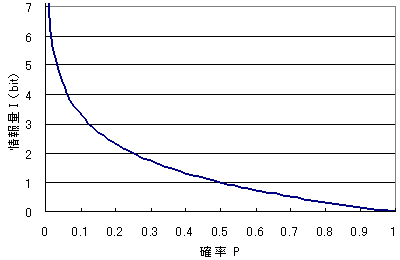
画像のエントロピーを単一の(スカラー)値で表すことが目的の場合は、を使用できますskimagemeasureshannon_entropy(grayImg)。 この関数は基本的に完全な画像に次の式を適用する: ここで、 グレーレベル(8ビット画像の256)の数であり、 グレーレベルを有するApr 04, エントロピーとは エントロピーは「乱雑さ」を表し、熱力学や統計力学でも出てきます。 また、エントロピーは画像の情報量を表す指標としても使われます。 画像のエントロピーの定義は以下のようになります。 画像の諧調(レベル)が 0 ~ (k1) の K値画像で、レベル i の出現確率が P i とすると、1画素の情報量は I = l o g 2 ( 1 / P i) = − l o g 2 P i b i t 1画面全体Jan 03, 15画像のファイルサイズはできるだけ小さく!! ⇒ 大きくても100KB程度を目安に。 1画素数を減らす ①トリミング: 必要な部分を残して切り取る ②縮小: 全体的に縮める 2減色: 色の数を減らす(24bit⇒8bit など) 3圧縮: 圧縮形式で保存(JPEG、GIFなど)
Sep 13, エントロピーと、生命、人類、宇宙の進化 生命、人類、宇宙に至る進化について記します。 を一つにまとめるように思えるからです。 量子力学の発展に寄与したシュレディンガーはまた生物学へも見識を広め、まだDNAの発見もされていない時代に、著書Jul 12, 192乗和誤差 損失関数として用いられる有名なものに2乗和誤差 (mean squared error)があります。 数式で表すと、 上の式において、 はニューラルネットワークの出力、 は教師データを表します。 上の式は教師データ (正解)の値とニューラルネットワークの出力実験1: 濃度分解能の異なる画像のエントロピーを測定してみよう. ImageJで対象画像を開くには,ImageJ起動後,File → Openで対象ファイルを指定する. ①LUTの変更 Image→Color→Edit LUT→Setを選択し,Number of Colorsを変える. 例えば,16とすると濃度分解能は4bit(16階調)になる. 1−1.濃度分解能 7bit, 6bit, 5bit, 4bit, 3bitの画像を作成し,それぞれのエントロピーを求




エントロピーとは 理系飯




エントロピー For Beginnersシリーズ イラスト版オリジナル 29 藤田 祐幸 槌田 敦 村上 寛人 本 通販 Amazon
エントロピー フィルター処理の実行 MATLAB コマンドの表示 この例では、 entropyfilt を使用したエントロピー フィルター処理の実行方法を説明します。 フィルター後のイメージ内の明るいピクセルは、元のイメージにあるエントロピーが高い近傍に対応します。 イメージをワークスペースに読み取ります。 I = imread ( 'circuittif' );Mar , 例えば,入力データが画像だとした時に,ラベルは「犬」「猫」の2つとするような場合です。 このとき,クロスエントロピーとは何を意味するのかというと, 「DNNの出力が得られた時に,ラベルが得られる確率にベルヌーイ分布を仮定したときの対数尤度」 を示します。そして、 (2)式は情報理論で云う画像の 平均情報量 のことでエントロピーと呼ばれています。



熱 エントロピー科学研究センター




小学生でも分かるエントロピーの話
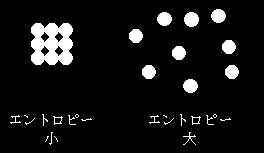
Sep 24, この場合、エントロピーは、「画素値が実際にどんな値をとるかの曖昧さ」を意味するわけですから、エントロピーが大きい画像とは、画素値のばらつきが大きい画像ですね。逆に、真っ白や真っ黒の画像は、エントロピーが小さいと言えます。 ② 相互情報量Dec 01, Binary Cross Entropy Lossは wikipedia によると下記の式で表されます。 先程の例で同様にp= 1, 0, 0に対してq= 07, 02, 01という予測が与えられた場合、Binary Cross Entropyは下記の通り計算できます。 こちらは、Cross Entropy Lossの時と違い、真値が0の時にも正しく分類Sep 18, すなわち、エントロピーを減少の方向へ導くことができれば、時間を逆方向に進むことも可能になる! という大胆な発想が『TENET テネット』の




エントロピーの概念の歴史から話そう エントロピーは 乱雑さ を意味するのか 宇宙に入ったカマキリ



トコトンやさしいエントロピーの本 第2版 エントロピー 熱力学 エネルギー ビジネス 化学 本 雑誌 日刊工業新聞
考察 結論 まとめ 1 はじめに 最近まれに、"エントロピー"という聞き慣れない言葉を耳にしますが、一体何なのでしょうか? ネットで良く見られるエントロピーの概念図 ネットで調べるといくらでも説明文が出てきますが、余りに難解でいくら読んでも結局良く分からないままではないでしょうか? 実際グーグルで検索すると、以下の説明文が真っ先に表示Sep 06, 交差エントロピーの意味 まず交差エントロピーは、以下の式で表されます。 $$E=\sum_{k}{{q(k)}log(p(k))}$$ pは、ニューラルネットワークで学習された確率。分類問題では学習データの正解率として出力されます。 qは、教師データの確率。エントロピーとは乱雑さの統計的尺度であり、入力イメージのテクスチャを特徴付けるために使用することができます。 エントロピーは sum (p*log2 (p)) で定義されます。 ここで、 p には imhist から返された正規化ヒストグラム数が格納されます。
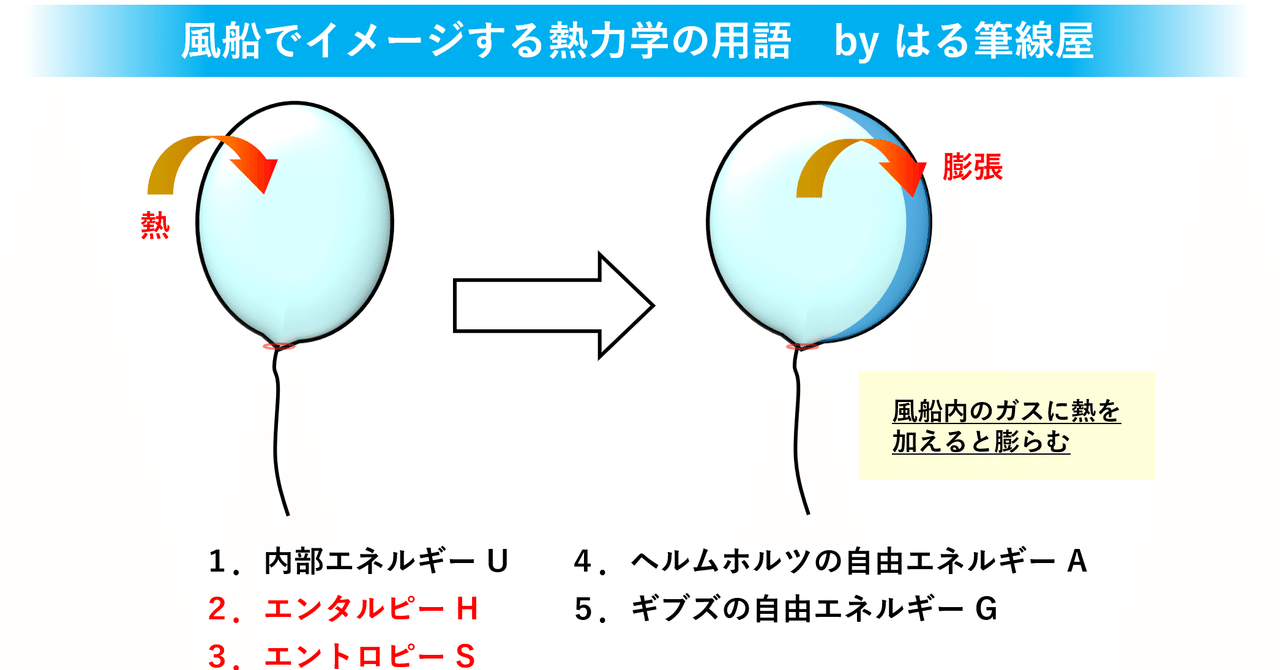



ぱわぽdeプレゼン 熱力学入門編に出てくる用語を自分なりの言葉でまとめてみたった 02 はる筆線屋 Note




エントロピーと秩序 熱力学第二法則への招待 ピーター W アトキンス 米沢富美子 森 弘之 本 通販 Amazon
–画像をある特徴が一様となる小領域に分割すること –画像から対象物を抽出し,その形や面積などを解析する など,画像認識の前処理として重要 •領域分割の方法 –領域拡張法 –統計的仮説検定法による領域拡張法 –ヒューリスティック法 –分割法ジタル画像における、H、S、Vそれぞれのエ ントロピーを計算した。なお、色を6色に分類 した場合のH座標の値のエントロピーを求め る式は、hをエントロピー、pを確率分布とす ると で表される。これは、ShannonWiener の多様 度指数とも呼ばれる。Jan 22, 18情報理論でとてもよく出てくる情報エントロピー。計算するにはどうすれば良いのだろう? 選択肢1:定義どおり作る 定義はとても簡単です。注意するべきことは、入力に0が来たときのパターンを想定しないで作るとmath domain errorが出る(は定義できないからね・・・)。




なぜエントロピーは乱雑さや情報量と呼ばれることがあるのか Kazelab
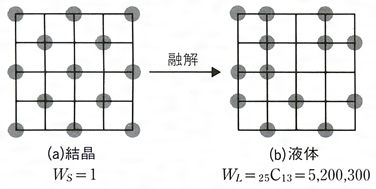



エントロピーとは コトバンク
様々なエントロピー 複数の事象系が互いに関係している場合に、それぞれの事象 系に関する様々なエントロピー(平均情報量)が定義できる。 次のようなゲのようなゲ ムをームを考える。 サイ ロゲ ム 「甲と乙がサイコロを振り合ってサイコロの目の大き画像dは画像cに与えるシャープフィルターを強くしたもので、最大エントロピー処理 によってできた、モコモコ斑点を強調しています(見るだけ!)。 画像e psf=25による2回目の最大エントロピー処理、画像を確認するためにシャープフィルターをEntropy は、画像のエントロピーを計算するMATLABの関数なので、ここで問題ありません。 @CitizenInsaneの回答で述べたように、 entropy グレースケール画像を1Dベクトルに展開し、この1Dベクトルにエントロピーのシャノン定義を適用します。




エントロピー Wikipedia



エントロピー カルバック ライブラー情報量 最尤推定法 初級mathマニアの寝言
エントロピー 符号化 逆変換 フレーム内 予測 予測 フレーム 対象 フレーム page 4 「前半:基礎の基礎」の内容 1 画像と符号化— 準備 2 画像の性質と符号化— 画素間相関と圧縮 3 エントロピー符号化 4 量子化 5 相関除去法(1) — 予測による方法 6すると、エントロピーの大きさが、得た情報の目安のひとつとして使えるはずである。 サービスの満足度について1万件の回答のうち、(悪い、やや悪い、ふつう、やや良い、良い)がそれぞれ (231, 1298, 3981, 2765, 1725) 件だったとすると、そのエントロピーは



情報量 エントロピー その性質の導出や証明 物理とか



情報エントロピー Emanの統計力学
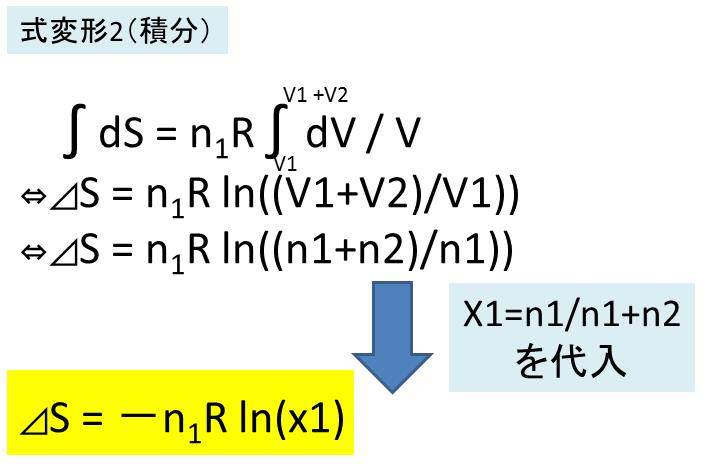



混合エントロピー 計算と導出方法は




大学物理 熱力学入門 エントロピー Youtube



B 2 数学的な一般化エントロピー
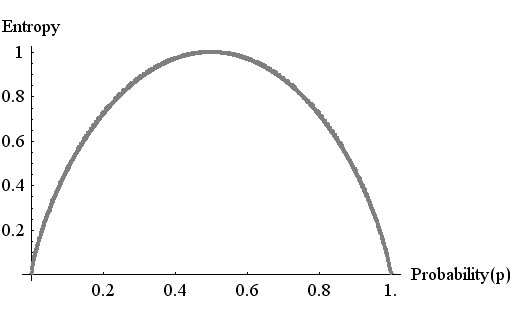



平均情報量 エントロピー
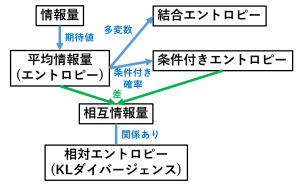



情報量とエントロピーに関する重要用語の整理 具体例で学ぶ数学




世界経済はエントロピー増大の法則への反逆 グローバルからリージョナルへ変質する不均衡 木走日記




エントロピー増大の法則を宇宙一わかりやすく物理学科の僕が解説する 物理学生エンジニア




エンタルピー エントロピー線図とは E M Jobs




エントロピー Yakugaku Lab



画像処理技法第9回




モルエントロピー S の温度依存性 図21 2 は物質によってどのくらい変わるのか Shinshu Univ Physical Chemistry Lab Adsorption Group




熱力学から見た エントロピー と エントロピー増大の法則 を理系ライターが丁寧に解説 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン




大学化学 エントロピーの定義 物理化学 熱力学 Definition Of Entropy Youtube




情報量って何 エントロピーの使い方を調べよう Itの学び




5分でわかる状態の乱雑さ エントロピーとの関係を理系学生ライターがわかりやすく解説 ページ 4 4 Study Z ドラゴン桜と学ぶwebマガジン




小学生でも分かるエントロピーの話




小学生でも分かるエントロピーの話




シリーズ 情報科学における確率モデル 5 エントロピーの幾何学 コロナ社



Calc Letter




エントロピー 単位



Physics Entropy




量子情報理論の基本 エントロピー 1 Qiita



5 1 自己情報量 情報エントロピー
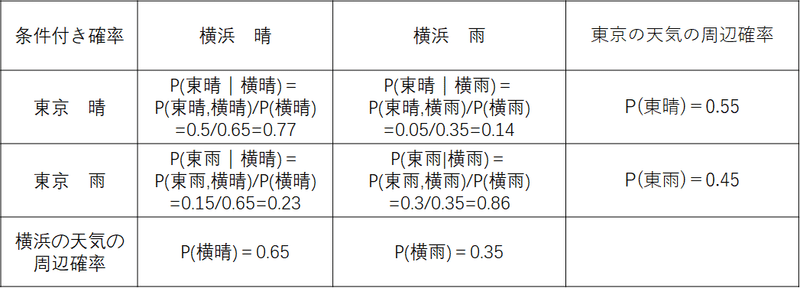



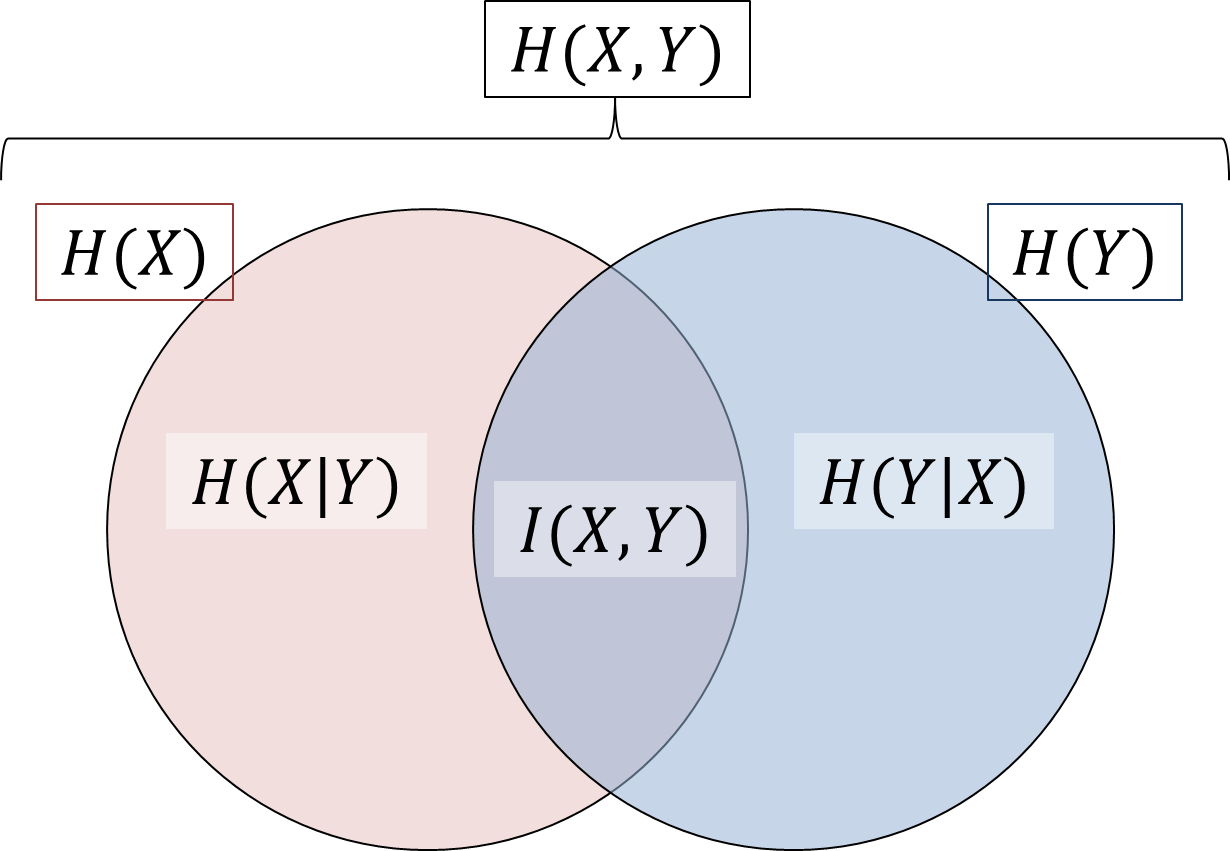
情報理論 第8回 条件付きエントロピー 結合エントロピー デジタルコミュニケーションさん Note




エントロピーから読み解く 生物学 めぐりめぐむわきあがる生命 漫画 無料試し読みなら 電子書籍ストア ブックライブ



エントロピー 計算 熱力学の基礎



エネルギー エントロピー



3



エントロピーで地球の生命を眺めてみる それはコーヒーに入れたミルクの かがやき 宇宙に果てはあるか 吉田 伸夫氏 07 毎日1冊 こちょ の書評ブログ



開催報告 第4回 理学の饗宴 しゅんぽじおん ーエントロピーとは ー 大阪大学大学院理学研究科附属基礎理学プロジェクト研究センター




情報エントロピーと自己情報量を初学者でもわかるように説明してみた 努力のガリレオ




エントロピー関数




画像のエントロピーをpythonで求めてみた Qiita



エントロピー 計算 熱力学の基礎




コース 物質が持つエネルギーの内訳 エントロピーと熱力学関数




5分でわかる状態の乱雑さ エントロピーとの関係を理系学生ライターがわかりやすく解説 ページ 3 4 Study Z ドラゴン桜と学ぶwebマガジン




エントロピーをめぐる冒険 初心者のための統計熱力学 鈴木 炎 ブルーバックス 講談社book倶楽部



熱力学におけるエントロピー



遺伝子とエントロピー




エントロピー 計算 熱力学の基礎



エントロピーの先に生命が見る夢と 世界と時間の美しさと 挑戦 元旦にこういうツイートをしたらたくさんリツイートしていただいたので せっかくなら By 高橋祥子 Medium




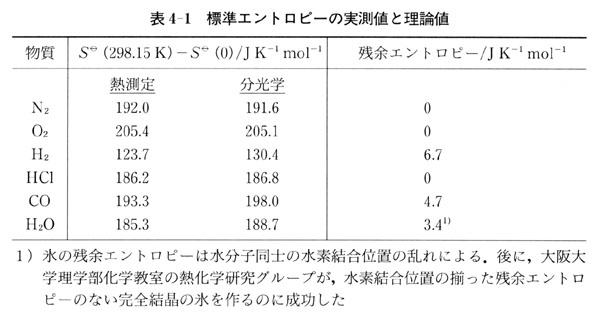
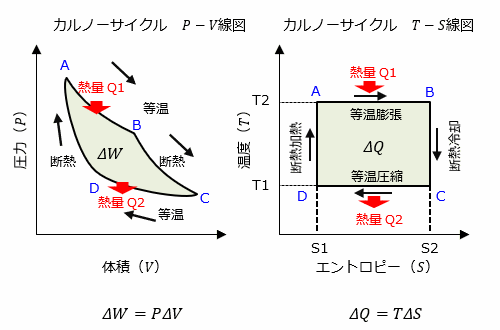
5分で分かる 熱力学第三法則 エントロピーやカルノーサイクルを用いて理系ライターが解説 Study Z ドラゴン桜と学ぶwebマガジン




5分でわかる状態の乱雑さ エントロピーとの関係を理系学生ライターがわかりやすく解説 ページ 3 4 Study Z ドラゴン桜と学ぶwebマガジン



1



エントロピーの意味をわかりやすく解説 統計力学と情報学の考えも ヒデオの情報管理部屋




3 物質のエントロピー



エントロピー増大の法則 哲学的な何か あと科学とか




図解 エントロピー増大の法則とは 自発変化の方向を示す熱力学の金字塔 Dreamscope Blog



簡単説明 エントロピーの法則とは ビジネスでも同じことが言える 売上を上げる集客ホームページ制作なら神奈川県藤沢市のソニド Sonido




エントロピー法則と経済過程 みすず書房




エントロピー増大の法則とは 分かりやすく良いもので例えてみた とはとは Net




エントロピーの先に生命が見る夢と 世界と時間の美しさと 挑戦 元旦にこういうツイートをしたらたくさんリツイートしていただいたので せっかくなら By 高橋祥子 Medium




エントロピーの定義式 Ds Dq Tの導出 化学に関するなんでもブログ




エントロピーが 時を戻す悪魔 を倒すまでの150年におよぶ戦い 高水 裕一 ブルーバックス 講談社 3 4




エントロピーの定義式についての質問です Clear



Q Tbn And9gcs3d59opr1i681fjlna1bugbbklc2gcyuuxgnzrlyn8yj3fpheg Usqp Cau




エントロピー増大の法則 石川県立大学 生化学 Youtube




Amazon 不規則性エントロピー 彩音 アニメ 音楽



京都大学大学院工学研究科材料工学専攻 乾 研究室




エントロピーが 時を戻す悪魔 を倒すまでの150年におよぶ戦い 高水 裕一 ブルーバックス 講談社 4 4



化学ポテンシャルのつりあいが 宇宙のエントロピーの変化がゼロ の式になる理由



1 エントロピーについて エントロピーと物質循環 地球環境問題への一つの視点 中澤 明 Seneca 21st



エントロピー 計算




建築環境のバイオクライトロジー エントロピーについて 環境建築 美しい省エネ住宅 エコハウススなら一級設計事務所 感共ラボの森



エントロピー



データ圧縮の向上 シャノン エントロピー の並列アルゴリズム Isus




小学生でも分かるエントロピーの話




熱力学におけるエントロピー




エントロピー えんとろぴー とは ピクシブ百科事典



エントロピー入門




レポート エントロピー増大の法則 エントロピーの話し 1




Pythonで0からディシジョンツリーを作って理解する 5 情報エントロピー編 Qiita




画像のエントロピーをpythonで求めてみた Qiita



エントロピーとは コトバンク




熱力学のエントロピーが難しいわけ 中小企業it担当者 菅雄一のブログ




相と系とエントロピー増大則 汚泥乾燥機 スラリー乾燥機 ヒートポンプ汚泥乾燥機 Kenki Dryer



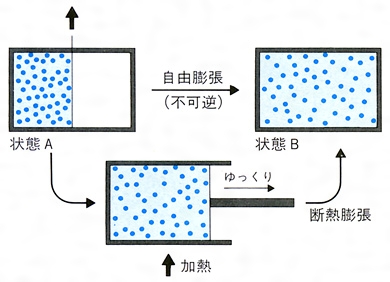
図解 エントロピー増大の法則とは 自発変化の方向を示す熱力学の金字塔 Dreamscope Blog



3




熱力学のエントロピーが難しいわけ 中小企業it担当者 菅雄一のブログ




エントロピー Yakugaku Lab




エントロピーが 時を戻す悪魔 を倒すまでの150年におよぶ戦い 高水 裕一 ブルーバックス 講談社 1 4




エントロピーと温度 圧力 濃度 粒子数との関係 化学に関するなんでもブログ
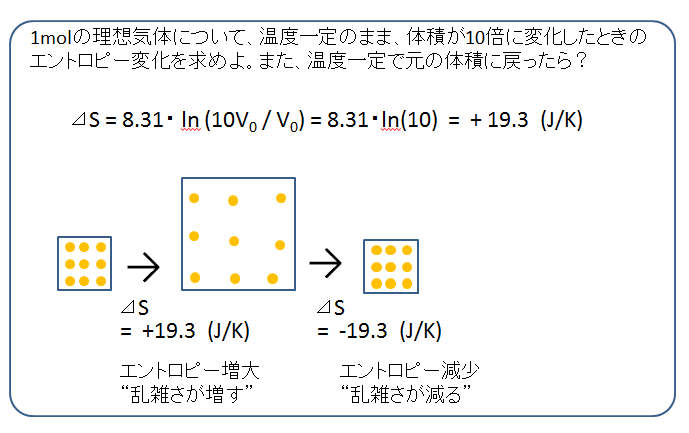
+%E6%B8%A9%E5%BA%A6+T+%E3%81%8C%E4%B8%80%E5%AE%9A%E3%81%AE%E9%81%8E%E7%A8%8B%E3%81%A7%E3%81%AF%E3%80%81.jpg)



エントロピー 計算 熱力学の基礎




エントロピー 計算 熱力学の基礎




5分で分かる 熱力学第三法則 エントロピーやカルノーサイクルを用いて理系ライターが解説 ページ 4 4 Study Z ドラゴン桜と学ぶwebマガジン



ときわ台学 化学熱力学 混合エントロピー 化学ポテンシャル




エントロピー とsdgs 第11回sdgs超実践者委員会 Sspc 月例会 ミートアップ 年10月23日 オンラインも同時開催 Eventregist イベントレジスト




エントロピー Youtube



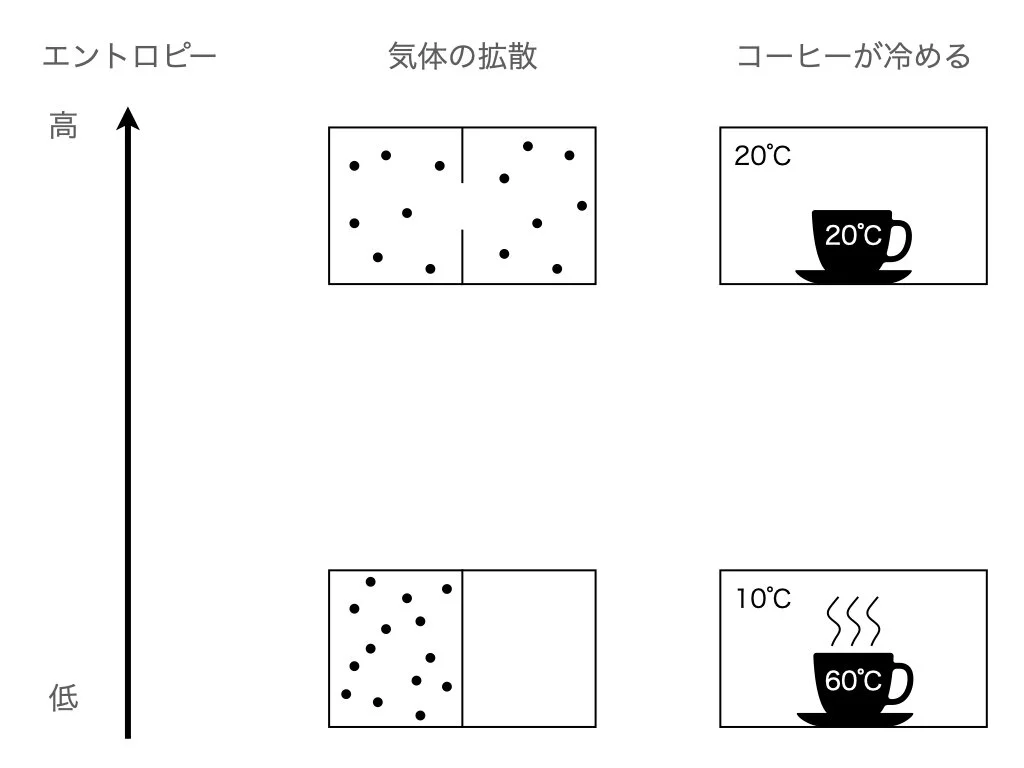
コース 物質が持つエネルギーの内訳 エントロピーと熱力学関数




自己情報量 エントロピー Kl情報量 交差エントロピーと尤度関数 Sambaiz Net



コメント
コメントを投稿